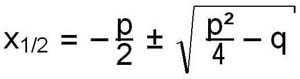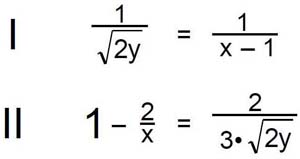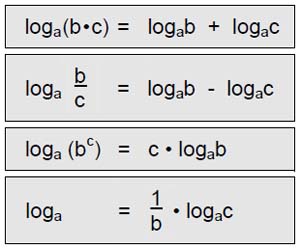Arbeitsblätter, Unterrichtshilfen und Klausuren zur Mathematik
Was Unterricht auch soll: Ein Zeitungsartikel von Kultusministerin Brunhild Kurth
Brandbrief der 130 Hochschullehrer gegen den zu frühen und zu häufigen Einsatz des Taschenrechners
Haft nach Streit um ein Matherätsel
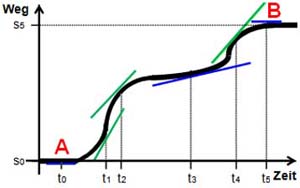
Differenzialrechnen 1 Die Eigenschaften von Zahlenfolgen
|
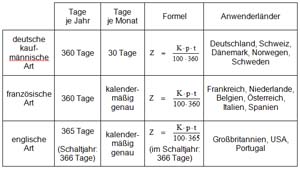
Diskontrechnen 1 Die Begriffe zum Diskontrechnen
|
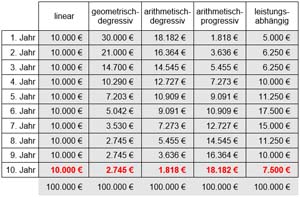
Die Formeln der Finanzmathematik wie Zinseszins, Annuitätendarlehen oder die Kreditzinsen-Berechnung scheinen für Schüler oft weit weg, sind aber für die Wirtschaft sehr bedeutsam.Finanzmathematik 1 Das Tilgungsrechnen
|
Gleichungen 0 Das Umstellen von Formeln
|
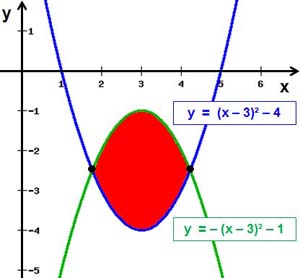
Integralrechnen Aufgaben zur Partialdivision
|
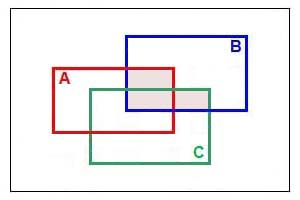
Kombinatorik
1 Die Produktregel
|
Das Leben ist kein Lotteriespiel.
|
Volumina berechnen |
Volumen (V) = A * h = Grundfläche * Körperhöhe |
Bei spitzen Körpern ist es ähnlich, nur dass das Ergebnis der oben genannten Formel durch 3 zu teilen ist.
Beispiel: die Berechnung des Volumens einer Pyramide
Volumen (V) = |
A * h |
= |
Grundfläche * Körperhöhe |
Bedeutsam ist eigentlich "nur" die Grundfläche des Körpers.
Sagt ein Schotte zum anderen: "Ich habe mir zwei Lose gekauft!" - Darauf der andere: "Was für eine Dummheit! Es gibt doch nur einen Hauptgewinn!"
Währungsrechnen Aufgabenblätter
1 - 14 |
Zahlensysteme 1 Einführung
|